1.简介
热膨胀效应:
(1)可以通过热膨胀系数(thermal expansioncoefficient)来定义,ABAQUS可以通过热膨胀系数来计算热应变;
(2)热膨胀效应可以是各向同性、正交异性或各向异性的;
(3)被定义为从参考温度(reference temperature)到计算温度产生的膨胀效应;
(4)可以被定义为一个依赖于温度和/或场变量的函数;
(5)在ABAQUS/Standard中,如果是连续实体单元,可以被定义为一个分布函数;
(6)在ABAQUS/Standard中可以直接使用用户子程序UEXPAN来定义(如果热应变是一个关于场变量和状态变量的复杂函数)。
2.计算热应变
ABAQUS通过热膨胀系数α来定义从参考温度θ0到计算温度θ产生的总的热应变,如图2.1所示。

图2.1 热膨胀系数的定义
产生的热应变可以通过下式进行计算:
其中:
α(θ,fβ)为热膨胀系数;
θ为当前温度;
θI为初始温度;
fβ为场变量当前的取值;
fβI为场变量的初始值;
θ0为热膨胀系数的参考温度;
上式中的第二项代表由于初始温度θI和参考温度θ0之间的温度差产生的热应变。这一项能够保证当参考温度不等于初始温度时初始热应变为0。
当热膨胀系数不为关于温度和场变量的函数时,可以不定义参考温度θ0。
3.热应变的转换
在ABAQUS中通常是以表格的形式来输入平均热膨胀系数。但有的时候,提供给你的热膨胀数据可能是以微分的形式来表示的:
即提供的是应变-温度曲线(如图2.1所示)的斜率。为了将这些数据转换为ABAQUS支持的平均热膨胀系数,需要进行一个从参考温度θ0到当前温度θ的积分运算:
例如,假设为一组常数值:dα1/dθ位于θ0和θ1之间;dα2/dθ位于θ1和θ2之间;dα3/dθ位于θ2和θ3之间;则有:
因此在ABAQUS中需要输入的平均热膨胀系数可表示为:
通过在ABAQUS/Standard中使用用户子程序UEXPAN可以定义与温度和/或场变量有关的热应变增量;如果热应变增量是与状态变量有关的函数,则必须使用用户子程序UEXPAN。
如果材料的热膨胀行为是各向同性的,则在用户子程序UEXPAN中只需要定义一个各向同性热应变增量(Δε=Δε11=Δε22=Δε33);如果是正交异性的,则需要定义热应变增量在三个主方向上的分量(Δε11,Δε22,Δε33);如果是各向异性的,则需要定义热应变增量的六个分量(Δε11,Δε22,Δε33,Δε12,Δε13,Δε23)。
4.热应力
如果一个结构不能自由膨胀,则温度的改变将会在结构内部产生应力。例如,考虑一个长度为L的杆单元,杆的两端被完全约束。横截面面积,杨氏模量E和热膨胀系数α均为常数。对于该一维问题,杆单元上产生的应力可以通过Hooke定律计算得到:
其中εx为总应变,εxth为热应变,Δθ为温度的该变量。由于杆单元是完全约束的,因此εx=0。如果杆单元两端节点的温度相同,则应力为:
受约束的热膨胀可以产生很大的应力值。对于典型的结构钢而言,150ºC的温度变化都将使得材料屈服。因此,在包含热载荷的问题中,应该非常小心地处理边界条件以避免对热膨胀造成过约束。
5.用户子程序UEXPAN
5.1简介
用户子程序UEXPAN:
(1)可以用于将热应变增量定义为关于温度、预定义场变量和状态变量的函数;
(2)被用于建立热应变与温度和/或预定义场变量和状态变量之间的复杂关系;可以在子程序中对热应变进行更新;
(3)将会在单元的所有积分点上被调用;
(4)在热力耦合分析中的每次迭代过程中,每个积分点会调用该子程序两次。
5.2用户子程序接口
SUBROUTINE UEXPAN(EXPAN,DEXPANDT,TEMP,TIME,DTIME,PREDEF,1
DPRED,STATEV,CMNAME,NSTATV,NOEL)CINCLUDE 'ABA_PARAM.INC'CCHARACTER*80
CMNAMECDIMENSION EXPAN(*),DEXPANDT(*),TEMP(2),TIME(2),PREDEF(*),1
DPRED(*),STATEV(NSTATV)user coding to define EXPAN, DEXPANDT and updateSTATEV if
necessary.RETURNEND
5.3可以定义的变量
EXPAN (*)
热应变的增量。热应变分量的数量和顺序取决于热膨胀行为的类型。
对于各相同性热膨胀,只需要定义一个分量;
对于正交异性热膨胀,需要定义Δε11th,Δε22th,Δε33th三个分量;
对于各相异性热膨胀,需要分别定义Δε11th,Δε22th,Δε33th,
Δε12th,Δε13th,Δε23th六个分量;如果是平面应力,则只需要定义Δε11th,Δε22th,Δε33th三个分量。
DEXPANDT (*)
热应变随温度的变化率,∂εth/∂θ。分量的数量和顺序取决于热膨胀行为的类型,与热应变增量类似。
5.4可以更新的变量
STATEV (NSTATEV)
用户自定义的状态变量。除了热力耦合分析,状态变量将会在增量步的开始时间被传递到子程序中,并可以在增量步结束时被更新。对于热力耦合分析,在每个积分点,每个增量步中子程序将被调用两次。在第一次调用时,状态变量的取值将会在增量步的初始时刻被传递到子程序中,并在增量步结束时被更新。在第二次调用时,第一次更新后的状态变量值将被再次传递到子程序中,并在增量步的结束时刻可以再次更新。
用户子程序UEXPAN允许热应变增量和状态变量是弱相关的。热应变对状态变量的导数不会包含在Jacobian矩阵中。
5.5用于获取相关信息的变量
TEMP (1)
当前温度(增量步的终止时刻)。
TEMP (2)
温度增量。
TIME (1)
增量步终止时刻对应的分析步时间。
TIME (2)
增量步终止时刻对应的总时间。
DTIME
时间增量。
PREDEF (*)
包含有所有用户自定义场变量的数组(分析开始时的初始值和当前的取值)。
CMNAME
用户指定的材料名称。
NSTATEV
与该材料有关的状态变量的数量。
NOEL
用户自定义单元号。
6.平均热膨胀系数的计算
图6.1为通过材料属性模拟软件JmatPro计算得到的SAE3140钢在冷却过程中奥氏体向马氏体转变的热应变温度曲线。
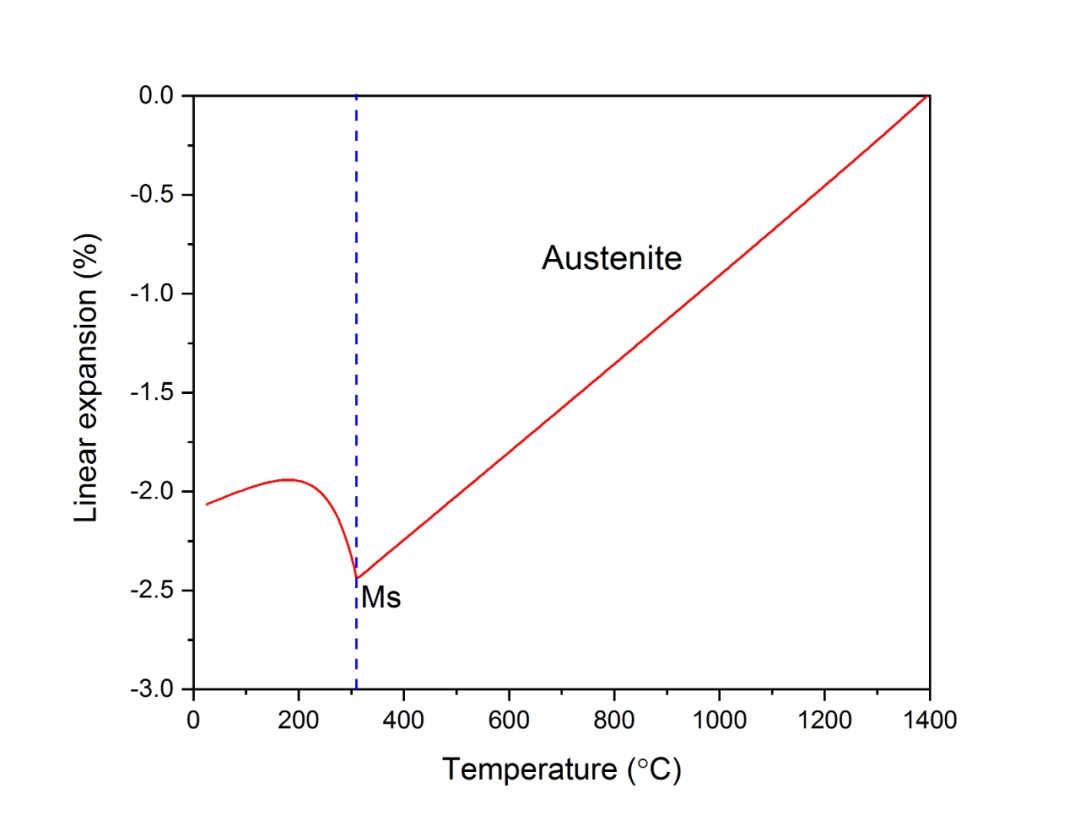
图6.1 热应变-温度曲线
从图6.1中可以看出随着温度的下降,材料产生热应变也随之降低,当温度下降到约300ºC时,热应变出现突然增长的现象,这是由奥氏体向马氏体转变过程中的体积膨胀引起的。因此该突变点对应的温度值即为马氏体转变开始温度Ms。
采用节3中的方法计算平均热膨胀系数:
其中ε0th为参考温度θ0对应的热应变,从图6.1中可以看出取值为0,αi为温度θi对应的平均热膨胀系数。
在Matlab中编制平均热膨胀系数的计算程序,如下所示。
%程序用于根据热应变温度曲线计算平均热膨胀系数exp_data=importdata('thermal_temp_curve.txt');
%导入热应变温度数据temp_data=exp_data(:,1); %温度数据strain_data=exp_data(:,2);
%热应变数据T_ref=1395; %参考温度strain_ref=interp1(temp_data,strain_data,T_ref);
%参考热应变sample_num=500;
%计算样点T=linspace(1300,25,sample_num)';strain=interp1(temp_data,strain_data,T);alpha=zeros(sample_num,1);%计算平均热膨胀系数for
i=1:sample_num alpha(i)=(strain(i)-strain_ref)/(T(i)-T_ref);endplot(T,alpha)
通过程序计算得到不同参考温度下以及JmatPro给出的平均热膨胀系数如图6.2所示。
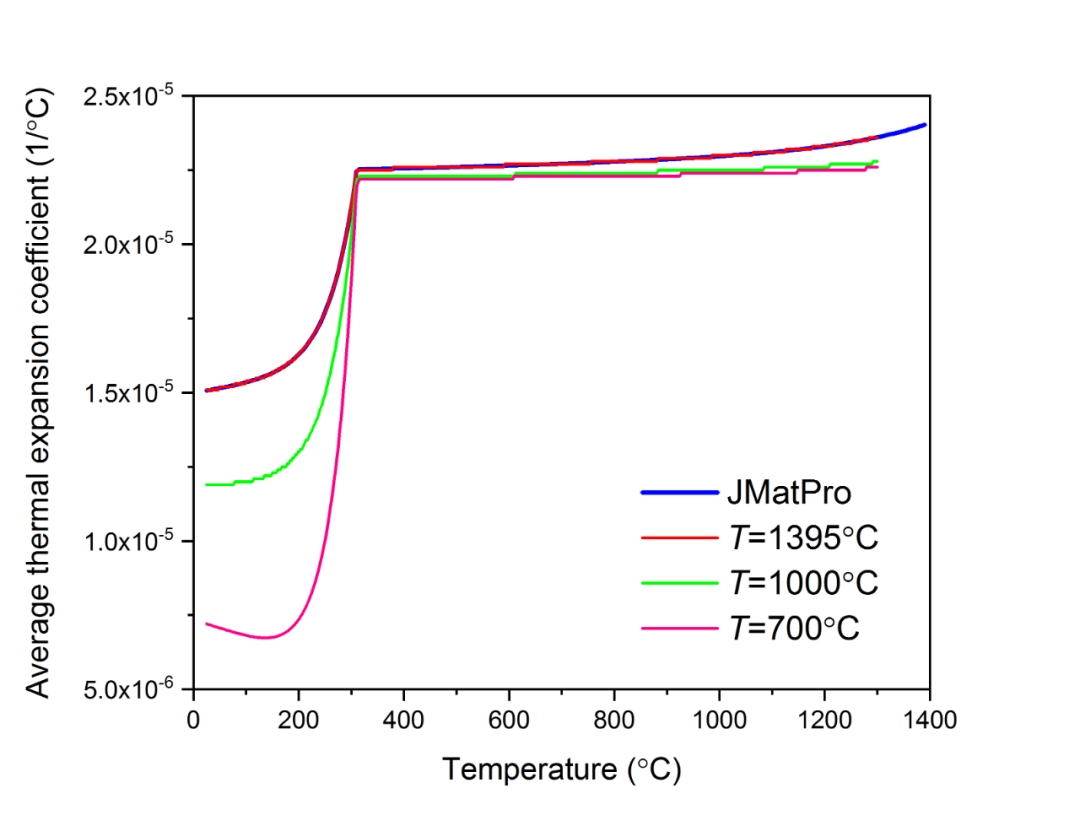
图6.2 平均热膨胀系数随温度变化
从图6.2中可以看出,当参考温度θ0取为1395ºC时,计算得到的平均热膨胀系数随温度的变化与JmatPro给出的结果几乎是重合的,这是因为JmatPro将应变为0的点(图6.1)对应的温度作为了参考温度。随着参考温度的变化,平均热膨胀系数也随之改变。因此,为了在ABAQUS中正确地定义热膨胀行为,必须准确地指定定义平均热膨胀系数所采用的参考温度,否则将无法获得正确的热应变值。
通过图6.2可以看出,当参考温度θ0取为某一值时,可以近似使得奥氏体和马氏体的热膨胀系数为一个不随温度变化的常数,如图6.2中的绿色曲线所示,当奥氏体几乎完全转变为马氏体之后,绿色曲线的末端近似为一条水平线,这代表着马氏体的热膨胀系数为一个常数值。而根据平均热膨胀系数的定义式不难看出,该参考温度的准确值可以通过如图6.3所示的方法进行求解。
首先用直线分别拟合对应奥氏体和马氏体体积分数为1时的热应变-温度曲线,两条直线的交点即为参考温度θ0。从图6.3中可以看出参考温度θ0约为881ºC。
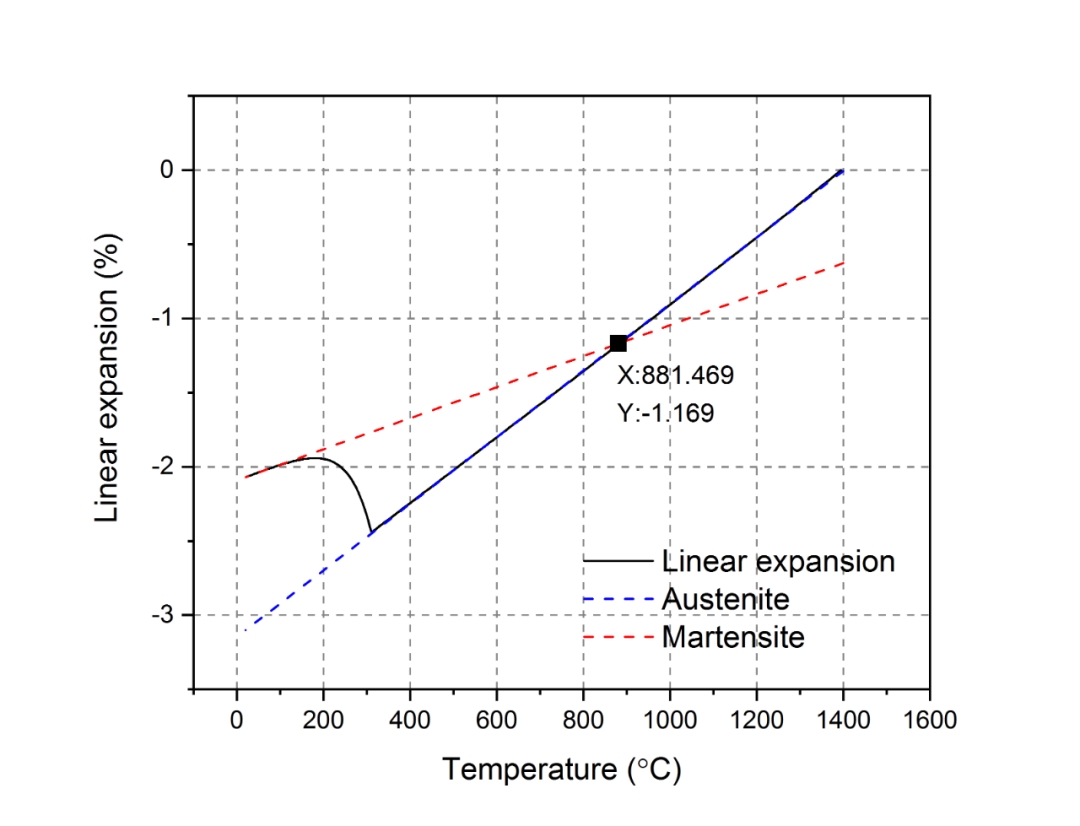
图6.3 参考温度的确定
两条直线的斜率即为奥氏体和马氏体的热膨胀系数,其取值如表6.1所示。
表6.1 奥氏体和马氏体的热膨胀系数

利用上面计算得到的参考温度重新计算平均热膨胀系数随温度的变化,结果如图6.4所示。
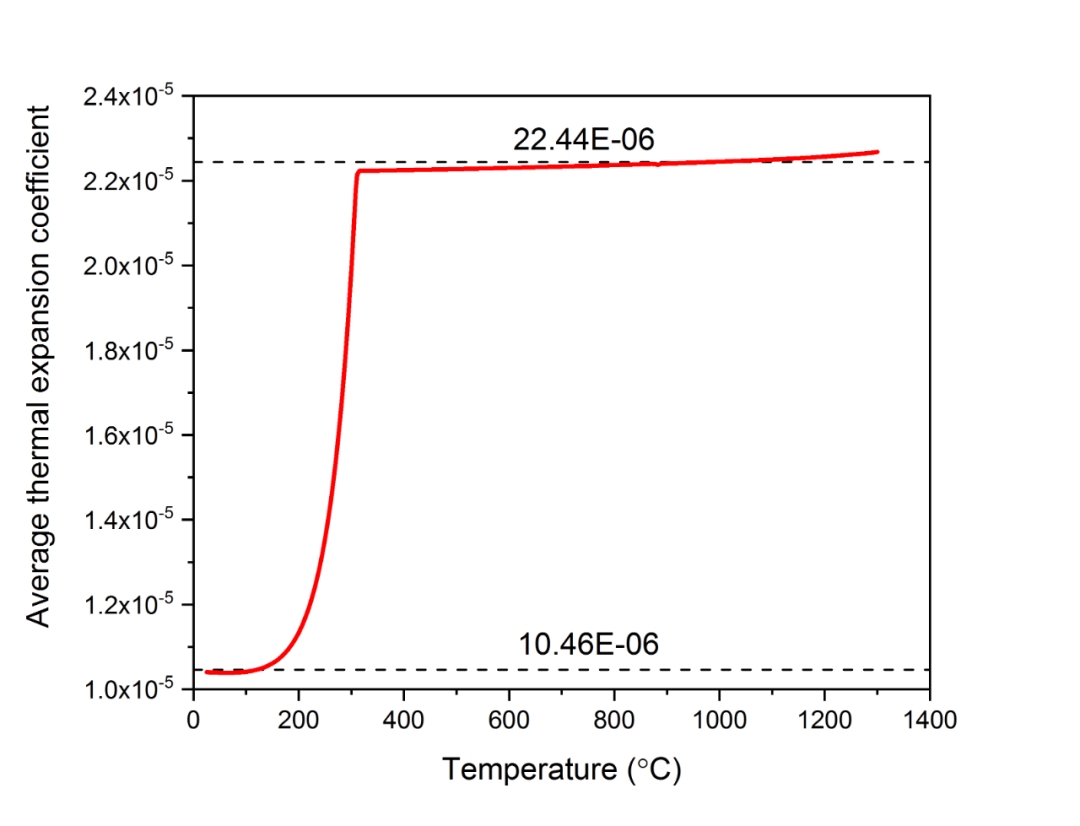
图6.4 平均热膨胀系数随温度的变化
图6.4中两条虚线分别代表奥氏体和马氏体的体积分数为1时的热膨胀系数,从图中可以看出,在使用了图6.3中确定的参考温度后,奥氏体和马氏体的热膨胀系数基本不随温度变化。换句话说,通过合理地选取参考温度,可以使得奥氏体和马氏体的热膨胀系数不随温度变化。
7.通过热膨胀系数计算热应变
通过上面分析过程可以看出,如果已知某一参考温度θ0下奥氏体和马氏体的平均热膨胀系数为一个不随温度变化的常数,以及奥氏体向马氏体转变过程中奥氏体和马氏体的体积分数(假定不存在扩散型相变),则可以直接计算如图6.1所示的热应变-温度曲线。
而奥氏体向马氏体转变的过程为非扩散型相变,可以通过Koistinen-Marburger模型来描述:
其中,vm和va分别为马氏体和奥氏体的体积分数,b为与材料有关的常数,Ms为马氏体转变开始温度。通过图6.1中的拐点可以大致判断出Ms约为300ºC。
常数b可以通过马氏体体积分数与温度之间的关系来确定,这里直接给出通过JmatPro计算得到的结果,如表7.1所示。

由上式可得奥氏体体积分数和温度之间满足关系:
因此,将奥氏体体积分数的自然对数与温度的数据进行线性拟合即可得到常数b的取值为0.019ºC-1,Ms取为310.5ºC,拟合曲线如图7.1所示。
在已知任意温度下奥氏体和马氏体的体积分数后,则对应的热膨胀系数可表示为:
热应变可表示为:
其中θI为初始时刻的温度,即热应变为0对应的温度值,在图6.1中θI为1395ºC。
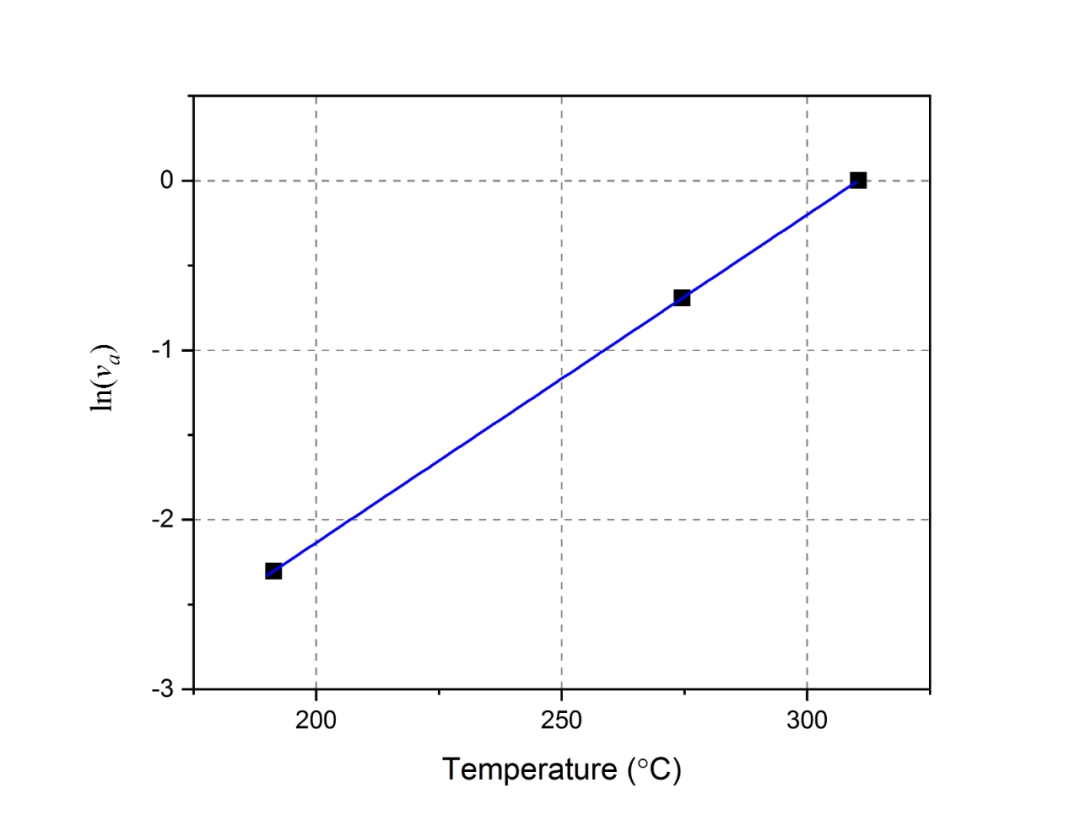
图7.1 拟合Koistinen-Marburger模型常数b
通过上述方法在Matlab中编写计算程序,如下所示。
%程序用于计算奥氏体向马氏体转变过程中的热应变随温度变化sample_num=200; %计算样点数CTE_a=22.44e-6;
%奥氏体热膨胀系数CTE_m=15e-6; %马氏体热膨胀系数T_ini=1395; %初始温度T_ref=881; %参考温度T_Ms=310.5;
%马氏体转变开始温度KM_b=0.019; %Koistinen-Marburger模型系数bVa=ones(sample_num,1);
%奥氏体体积分数Vm=zeros(sample_num,1); %马氏体体积分数alpha=zeros(sample_num,1);
%热膨胀系数strain=zeros(sample_num,1); %热应变T=linspace(1400,20,200)'; %温度for
i=1:sample_num %计算奥氏体和马氏体体积分数 if T(i)<=T_Ms Vm(i)=1-exp(-1*KM_b*(T_Ms-T(i)));
Va(i)=1-Vm(i); end %计算热膨胀系数 alpha(i)=Vm(i)*CTE_m+Va(i)*CTE_a; %计算热应变
strain(i)=alpha(i)*(T(i)-T_ref)-...
alpha(i)*(T_ini-T_ref);endfigure;plot(T,Vm,T,Va);figure;plot(T,alpha);figure;plot(T,strain);
计算得到的热应变随温度的变化如图7.2所示。
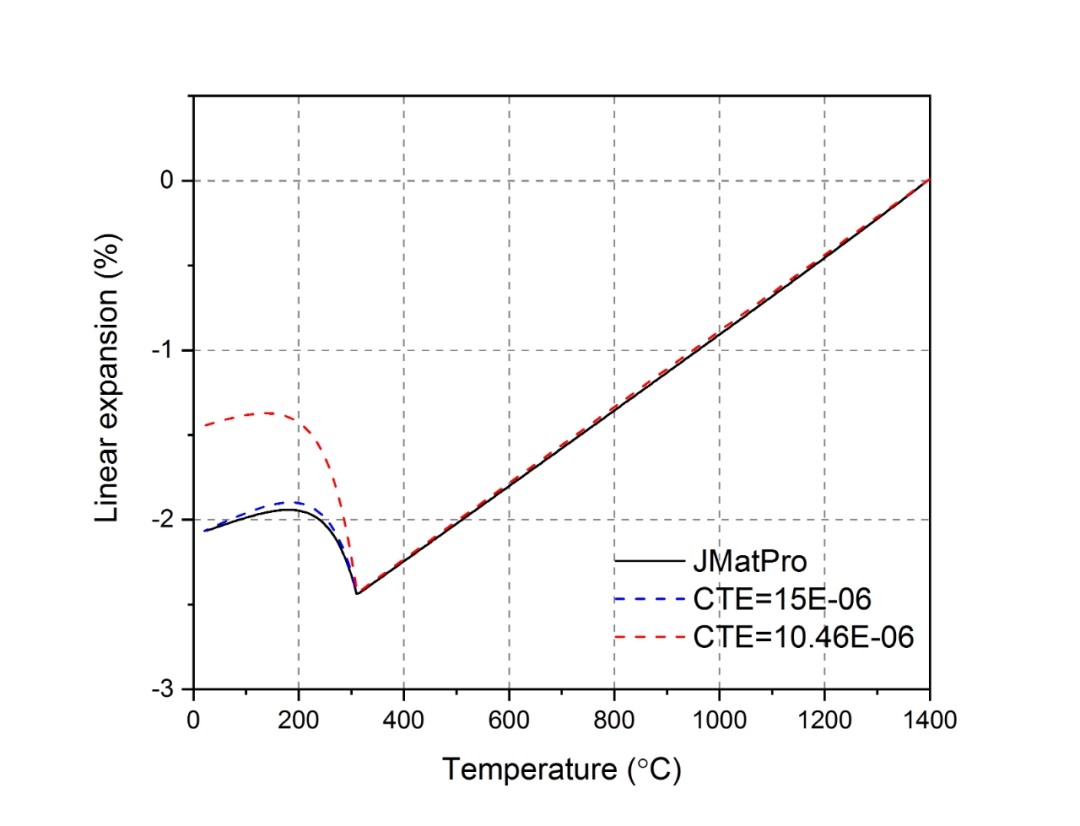
图7.2 热应变-温度变化曲线
图7.2中黑色曲线为通过JmatPro计算得到的热应变曲线,红色曲线为马氏体热膨胀系数取值为10.46×10-6ºC-1时计算得到的热应变曲线,该热膨胀系数值是通过拟合JmatPro给出的热应变曲线得到的,但似乎与黑色曲线有较大的差异;反而是将马氏体热膨胀系数取值为15×10-6ºC-1时与黑色曲线较为吻合,本文认为这主要是由于拟合直线斜率时温度范围选取不当引起的。在拟合马氏体的热膨胀系数时,本文选取了20ºC~200ºC的温度范围,而从表7.1中可以看出,当温度位于200ºC时,此时马氏体的体积分数为90%,因此此时对应的热膨胀系数并非马氏体体积分数为100%时的热膨胀系数。如果采用该温度段进行拟合,将造成拟合得到的热膨胀系数偏小。如果缩小拟合时选取的温度范围,预计能够获得较好的结果。皮特宠物博客
(素材来自网络,侵删)